Macros for the Determiners
Determiners get a slightly more complex semantics. Here are the semantic macros for ``every'' (with the label uni) and ``a'' (with label indef):
detSem(uni,usr([Root,N1,N2,N3,N4,N5,N6,N7,N8,N9],
[Root:lambda(N1),N1:lambda(N2),N2:forall(N3),N3:(N4 > N5),
N4:(N6@N7),N5:(N8@N9),N6:var,N7:var,N8:var,N9:var],
[],
[bind(N6,Root),bind(N7,N2),bind(N8,N1),bind(N9,N2)])).
detSem(indef,usr([Root,N1,N2,N3,N4,N5,N6,N7,N8,N9],
[Root:lambda(N1),N1:lambda(N2),N2:exists(N3),N3:(N4 & N5),
N4:(N6@N7),N5:(N8@N9),N6:var,N7:var,N8:var,N9:var],
[],
[bind(N6,Root),bind(N7,N2),bind(N8,N1),bind(N9,N2)])).
These structures look quite intimidating, but if you look at the corresponding constraint graphs, you'll see that e.g. the macro for ``every'' is nothing but a description of the term 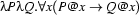 . To make it easier to check that the semantic macro
. To make it easier to check that the semantic macro detSem(uni,...) given above really corresponds to this tree representation, we have decorated the tree backbone with the respective PROLOG-variables (see below on the right).

Just in order to make life easier for us from now on, we'll abbreviate the graphs for determiners as follows:

We can do this safely because the root of the subgraph is the only node we'll have to refer to below.