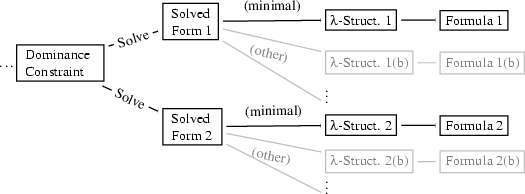
4.1.2 Solved Forms

Many solutions...

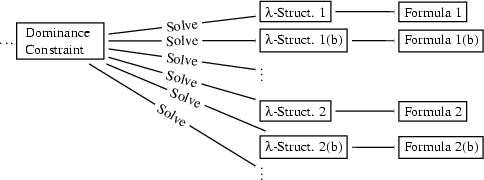
In fact, if you think about the enumeration problem a bit, you'll notice that it is not realistic to enumerate all 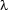-structures that solve the constraint: In general, there can exist an infinite number of satisfying 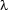-structures into which the fragments can be embedded while respecting the dominances. However, the differences between most of the solutions are completely irrelevant additions of extra material. The situation looks like this:

In this example, we might only be interested in the two solutions 1 and 2 while the "variants" 1(b) and 2(b) as well as all other variants with additional material inbetween are pointless to us.

...few solved Forms

So instead of really trying to enumerate solutions (i.e. 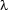-structures), we reformulate the problem to enumerate solved forms of the original constraint. Intuitively, solved forms are themselves constraint graphs that each represent a class of solutions that only differ in the addition of extra material. We will define them in a way that they have the following useful properties:

• Every constraint graph has a finite number of solved forms.

• The solutions of all solved forms of a constraint taken together are the same as the solutions of the original constraint.

• It is trivial to enumerate the solutions of a solved form.

Before we look at an example, let's refine the scheme of our architecture once more: