1.1 Introduction
Meaning Representations
Before looking at the details of semantics construction, there's one big question that we have to answer: Meaning as such is a very abstract concept. It's not at all easy to imagine what it is to ``get to the meaning'' of a sentence, let alone to ``construct'' it from that sentence. To study meaning, and especially to deal with it on a computer, we need a handle on it, something more concrete: We shall work with meaning representation s - strings of a formal language that has technical advantages over natural language. In this chapter, we will represent meanings using formulas of first-order logic.
For instance, we will say that the meaning of the sentence ``Every man walks'' is represented by the first order formula 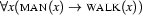 , and that the formula
, and that the formula 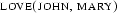 represents the meaning of the natural language sentence ``John loves Mary''.
represents the meaning of the natural language sentence ``John loves Mary''.
So basically, this chapter will be concerned with finding a systematic way of translating natural language sentences into formulas of first order logic (and writing a program that automates this task). Here's what we will do:
We will start with a very short repetition of some central concepts of first order logic.
Then, we will show how to represent first order formulas - thus, our target representations - in Prolog.
Next, we will discuss theoretically some of the basic problems that arise in semantic construction, introduce
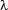 -calculus, and show why it is our tool of choice for solving these problems.
-calculus, and show why it is our tool of choice for solving these problems.Finally we will turn to our implementation: We give Prolog code for the basic functionalities of
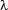 -calculus, and then show how to couple
-calculus, and then show how to couple 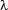 -based semantic construction with our first, DCG-based, parsing-predicates.
-based semantic construction with our first, DCG-based, parsing-predicates.