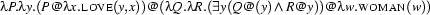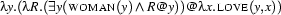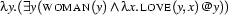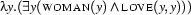1.4.7 [Sidetrack:] Accidental Bindings

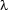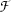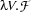But before we can put -calculus to use in an implementation, we still have to deal with one rather technical point: Sometimes we have to pay a little bit of attention which variable names we use. Suppose that the expression in is a complex expression containing many 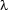operators. Now, it could happen that when we apply a functor 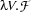to an argument 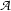, some occurrence of a variable that is is free in 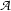becomes bound when we substitute it into .

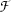For example when we construct the semantic representation for the verb phrase ``loves a woman'', syntactic analysis of the phrase could lead to the representation:

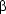-reducing three times yields:

Notice that the variable occurs 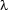-bound as well as existentially bound in this expression. In 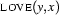it is bound by 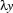, while in 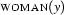and it is bound by 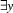. So far, this has not become a problem. But look what happens when we 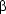-convert once more:

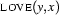has been moved inside the scope of 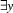. In result, the occurrence of has been 'caught' by the existential quantifier, and 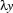doesn't bind any occurence of a variable at all any more. Now we 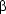-convert one last time and get:

We've got an empty 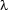-abstraction, made out of a formula that means something like ``A woman loves herself''. That's not what we want to have. Such accidental bindings (as they are usually called) defeat the purpose of working with the 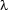-calculus. The whole point of developing the 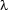- calculus was to gain control over the process of performing substitutions. We don't want to lose control by foolishly allowing unintended interactions.