1.2.6 Representing formulas in Prolog

We would like to use first order logic as a semantic representation formalism, and we want to deal with it in Prolog. So the next thing we need is a way of writing down formulas of first-order logic in Prolog. In short, we will simply use Prolog terms for this purpose that resemble the formulas they stand for as closely as possible. This is what we deal with in this section.

Atomic Formulas

First, we must decide how to represent constant symbols, predicate symbols, and variables. We do so in the easiest way possible: a first-order constant will be represented by the Prolog atom c, and a first-order predicate symbol will be represented by the Prolog atom p. Variables will also be represented by Prolog atoms. Note that this choice of representation won't allow our programs to distinguish constants from variables. So it's our own responsibility to choose the atoms for constants distinct from those for variables when we write down formulas in Prolog.

Given these conventions, it is obvious how atomic formulas should be represented. For example, would be represented by the Prolog term love(john,mary), and 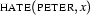would be represented by hate(peter,x).

Complex Formulas

Next for Boolean combinations of simple formulas. The symbols

&       v       >       ~

will be used to represent the connectives 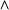, , 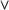, 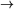and respectively.

The following Prolog code ensures that these connectives have their usual precedences:

 :- op(900,yfx,>).         % implication
 
 :- op(850,yfx,v).         % disjunction
 
 :- op(800,yfx,&).         % conjunction
 
 :- op(750, fy,~).         % negation

Have a look at Learn Prolog Now! if you are unsure about what this code means.

Here are some examples of complex first-order formulas represented in Prolog. To test your understanding of the above operator definitions: How would the formulas look in fully bracketed version?

• love(john, mary) & love(mary, john) > hate(peter,john)

• love(john, mary) & ~ love(mary, john) > hate(john.peter)

• ~ love(mary, john) v love(peter,mary) & love(john, mary) > hate(john.peter)

Quantifiers

Finally, we must decide how to represent quantifiers. Recall that the first order formula 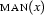has the Prolog-representation man(x). Now 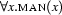will be represented as

forall(x,man(x))

and 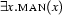will be represented as

exists(x,man(x))